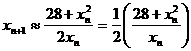APROXIMACIONES SUCESIVAS

La Raíz Cuadrada.

¿Te has preguntado cómo es que una calculadora hace sus cálculos? Por ejemplo, calcular la raíz cuadrada de un número dado, en las calculadoras científicas siempre encontrarás una tecla para la raíz cuadrada, sólo debes oprimirla para encontrar la raíz de cierto número.

La raíz cuadrada de un número es otro número que al elevarse al cuadrado nos dé como resultado el número del cual estamos obteniendo la raíz cuadrada, por ejemplo, 4 es la raíz cuadrada de 16 ya que . El número 32 no es el cuadrado de ningún número natural, su raíz cuadrada en consecuencia no es un número natural, sin embargo podemos decir que 6 es una aproximación a la raíz cuadrada de 32 ya que , lo mismo podríamos decir de el número 5 ya que , en el primer caso diremos que 6 es una raíz cuadrada inexacta por exceso de 32, ya que y en el segundo caso que 5 es una raíz cuadrada inexacta por defecto de 32 ya que , de una cosa si estamos seguros: la raíz cuadrada de 32 está entre el 5 y el 6.

Extracción de raíces cuadradas por aproximaciones sucesivas.

Supongamos que necesitamos obtener la raíz cuadrada de 28. Sabemos que la raíz cuadrada de este número está entre 5 y 6, en efecto: . Elijamos un valor aproximado de esta raíz, por ejemplo y designemos con al error que se comete con esta aproximación, así

Para determinar el valor de , elevemos al cuadrado los dos miembros de la igualdad

y arreglando de manera conveniente

hemos obtenido una ecuación cuadrática para

Ahora haremos la siguiente consideración: Como el error es menor que 1, es menor que , hallemos entonces un valor aproximado del error despreciando de la igualdad , esto es

De la ecuación anterior se deduce que , luego

Hemos encontrado, entonces un valor “mas aproximado” a la raíz cuadrada de 28, llamemos a este valor aproximado de la raíz cuadrada y repitamos el procedimiento para hallar una aproximación mejor a la raíz cuadrada designando con .al error que se comete con este valor aproximado.

elevando al cuadrado

despreciando el término por ser menor (y por lo tanto menos significativo) que .

La tercera aproximación a la raíz cuadrada de 28 será:

Repitiendo el procedimiento para una mejor aproximación, designando con al error cometido con el valor aproximado.

observa que la expresión de arriba es similar a la expresión inicial de la iteración anterior, por lo cual, al repetir el procedimiento nos conducirá a

Hemos encontrado un patrón que nos permite escribir una expresión general para cada iteración que nos conduce a una mejor aproximación, ésta es

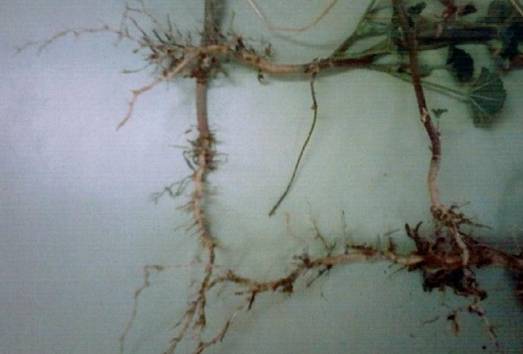
Si generalizamos más esta estrategia no sólo para hallar la raíz cuadrada de 28 sino la de cualquier número a, la expresión de arriba se transforma en

Usando la tecnología.

La expresión obtenida para aproximar la raíz cuadrada de un número requiere siempre de una aproximación anterior, esto es, para hallar la enésima mas una aproximación necesitamos haber obtenido la enésima aproximación. Utilizaremos la tecnología para aproximar la raíz cuadrada de un número utilizando la expresión hallada anteriormente.

En una computadora usaremos una hoja de cálculo electrónica, ésta contiene filas y columnas en las cuales se pueden definir fórmulas. La hoja de cálculo se visualizará así:

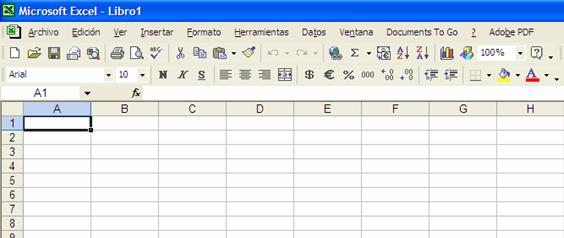
En la primera fila de la hoja escribamos en las columnas A, B y C, respectivamente a, Xn y Xn+1 para identificar cada una de las celdas, en este hoja de cálculo una celda se identifica con una letra y un número, la letra se refiere a la columna y el número a la fila donde se localiza la celda, la celda activa se muestra enmarcada con una linea mas gruesa que las demás.

Por ejemplo en la siguiente pantalla se observa remarcada la celda C4, que corresponde a la columna C fila 4

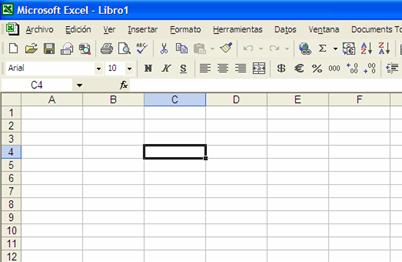
Escribamos pues a, Xn y Xn+1 en las celdas A1, B1 y C1 respectivamente

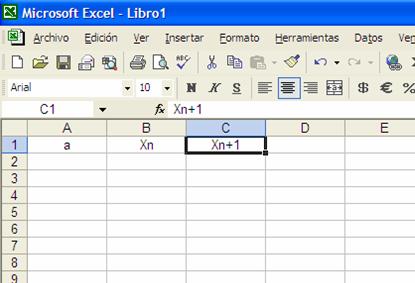
En la celda A2 estaremos introduciendo el valor del número al cual queremos hallar su raíz cuadrada, en la celda B2 introduciremos la primera aproximación de la raíz cuadrada, esto es y en la celda C2 escribiremos nuestra fórmula para hallar la segunda aproximación, esto es

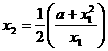
La sintaxis para escribir la fórmula en la hoja de calculo es la siguiente:

=0.5*(A2+B2*B2)/B2

El signo igual antes de la expresión indica que lo que está escrito es una fórmula, A2 es una variable que será igual al valor que se introduzca en la celda C2, en nuestro ejemplo el valor de a (número al que se le desea extraer raíz cuadrada), B2 es una variable igual al valor introducido en esa misma celda ( la primera aproximación a la raíz), la fórmula también podría haberse escrito

=0.5*(A2+B2^2)/B2

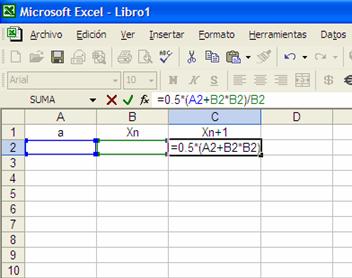
Después de escribir la fórmula oprimimos la tecla “enter” y la hoja de calculo nos muetra lo siguiente

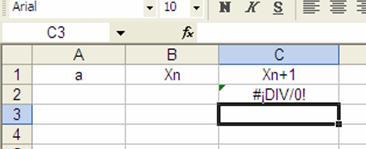
Cómo aún no introducimos el valor de a en A2 ni el valor de en B2, la hoja de cálculo los considera 0 y la expresión mostrada en C2 nos indica que existe una división entre cero.

Introduzcamos los valores de a en A2 y de en B2, elijamos para ello los mismos usados en nuestro ejemplo, esto es 28 (número al que hay que encontrar la raíz cuadrada) y 5 (primera aproximación a la raíz), respectivamente, nuestra hoja de cálculo tendrá ahora la siguiente apariencia.

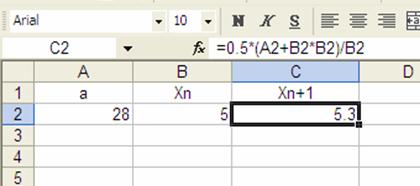
donde ahora en la celda C2 se observa el valor calculado por la fórmula, esto es 5.3.

En la celda B3 introduzcamos, ahora, el valor de que corresponde al valor presentado en la celda C2, esto es 5.3. Para ello escribamos en la celda B3 lo siguiente

=C2

esto indica que el valor que le corresponde a esta celda (B3) es el calculado en la celda C2. La hoja de cálculo lucirá así:

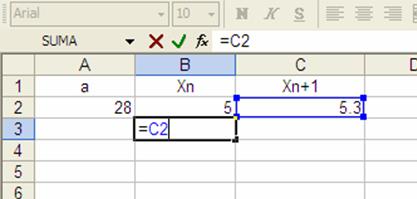
y después de oprimir “enter” en B3 aparecerá el mismo valor que en C2, esto es 5.3.

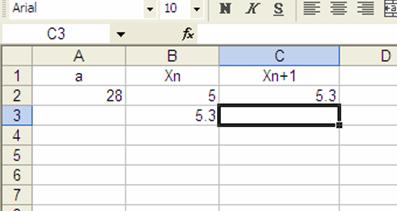
en C3 debemos volver a escribir nuestra fórmula para la siguiente aproximación, sin embargo, como esta es la misma (sólo que válida para los valores de la fila 3) que la inmediatamente superior, bastará copiar la fórmula, para ello debemos situarnos en la celda de la fórmula a copiar (C2) y posicionar el puntero del “ratón” en el pequeño cuadrito situado en la esquina inferior izquierda hasta que éste se transforme en una cruz, en ese momento oprimir el botón del “ratón” y “arrastrar” hasta la celda de abajo y soltar el botón, inmediatamente se desplegará el resultado en la celda C3. Posicionémonos en la celda C3 y revisemos la celda copiada

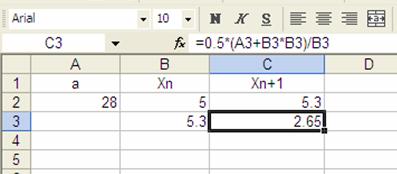
El valor obtenido no es el esperado, esto se debe a que en la nueva fórmula aparece el valor de la celda A3 (=0.5*(A3+B3*B3)/B3) que en nuestra hoja al no existir se considera como cero (y no 28 como debe ser). Recordemos que esa entrada corresponde al número del cual queremos conocer su raíz cuadrada y que esta permanece constante en cada una de las iteraciones. Escribamos en esta celda el mismo valor que tenemos en la celda de arriba, para ello podríamos simplemente introducir el número 28 o, mejor, indicar que en esta celda se copiará el valor de la celda de arriba, esto lo hacemos simplemente escribiendo

=A2

que indica que el valor en esta celda será el mismo que en A2

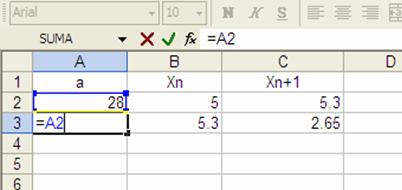
y después de oprimir “enter”

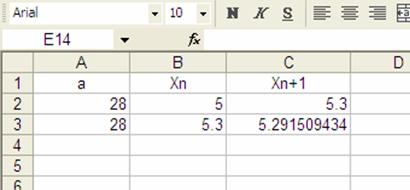
tenemos ya definidas todas las fórmulas para la fila 3, esto es para las celdas A3, B3 y C3. Podemos copiar estas tres fórmulas a los renglones de abajo, para ello marcaremos las tres celdas a copiar y siguiendo el mismo procedimiento de arrastrar y soltar podemos copiarla a las filas de abajo, arrastrabdo el “ratón” hacia abajo cubriendo todas las filas donde queremos copiar y soltar el botón una vez que hallamos terminado la selección. Por ejemplo, la hoja siguiente exhibe las fórmulas copiadas hasta la fila 20.

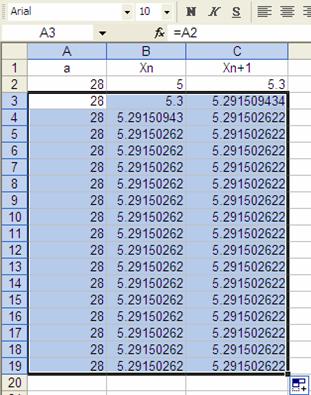
Observa como una aproximación hasta de 9 cifras decimales se obtiene ya en la iteración 3. Tenemos lista nuestra hoja de calculo, ahora sólo deberás introducir el valor del número al que quieras obtener su raíz cuadrada en la celda A1 y la primera aproximación en B1. Por ejemplo para aproximar , introduzcamos los datos:

la hoja de datos se mostrará así

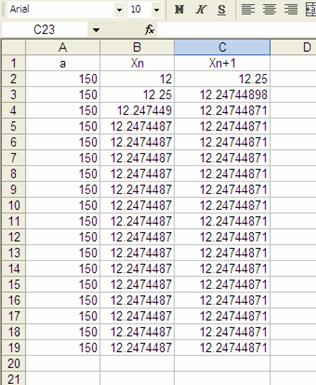
Recuerda que nuestra estrategia que dio origen a la fórmula iterativa se basaba en que el error era en cada paso menor que 1 y esto era porque podíamos establecer que el valor exacto de la raíz cuadrada se hallaba entre dos números naturales consecutivos, esto es:

, o

o como en el último ejemplo empleando la hoja de cálculo

eligiendo el menor de los números naturales consecutivos entre los cuales se encuentra la raíz, garantizamos que el error en la aproximación sea y por tanto razón por la cuál en nuestro proceso de construcción de la fórmula podíamos despreciar el valor .

Los ejemplos trabajados son sencillos y casi por simple inspección podemos dos números naturales consecutivos entre los cuales está la raíz cuadrada de número en cuestión, sin embargo si quisiéramos obtener la raíz cuadrada de 1234567890, es difícil establecer a priori entre cuáles dos números naturales consecutivos se encuentra el valor de la raíz y por lo tanto elegir el menor de estos para nuestra primera aproximación y garantizar que el error sea menor que1.

¿Qué sucede con nuestro método si elegimos como primera aproximación un número en el cuál el error entre éste y el valor de la raíz sea mayor que 1?

La pregunta del párrafo anterior se plantea ya que al ser , y de acuerdo a nuestro procedimiento estaríamos despreciando un valor más significativo del que conservamos. ¿Crees que funcionaría el método? En nuestra hoja de cálculo podemos ensayar varios casos. Construye una explicación según sea el caso observado.